说明

二叉搜索树（Binary Search Tree） BST  , 文中使用 BST 都代表二叉搜索树。

BST 结构 

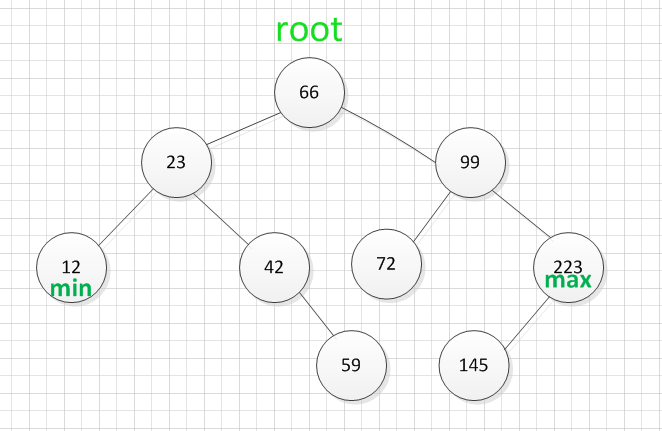
根节点  （root）： BST 最顶端的节点 。

父节点 ： 任意节点 K 的上层节点 。

叶节点 ： 没有子节点的节点 。

左子树 ： 任意节点 K 左侧的 BST 。

右子树 ： 任意节点 K 右侧的 BST 。 

这种数据结构比线性的结构的数组在删除，插入方面有更好的性能。比线性结构的链表在查找方面有更好的性能。

BST 特性

一颗二叉树只有符合 BST 的特性时才是一颗 BST 。无论对BST对任何操作都不能使其违反了BST的特性（要保持住BST的结构），否则该二叉树将不再是一颗BST。

1. 任意节点 K 的左子树的所有节点都小于节点 K （当且仅当K节点左子树不为空时）。

2. 任意节点 K 的右子树的所有节点都大于节点 K （当且仅当K节点右子树不为空时） 。 

3. 任意节点 K 的左子树，右子树都是 BST （也就是一颗 BST 中所有的子树都必须符合BST的特性） 。

4. 不存在键值相等的节点 。

BST 动态演示

• 插入

• 查找

• BST 转换为有序数组

BST 的最好，典型，最坏情况

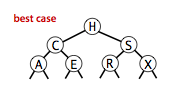
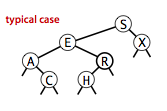
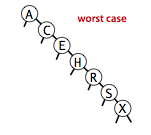
BST 的性能取决于树的高度 ，树的高度取决于节点的插入顺序和元素本身的大小。